-
그래프의 탐색 DFS, BFSData Structure & Algorithm 2020. 10. 6. 08:20반응형
그래프의 모든 노드를 탐색하는 방법으로 DFS(Depth First Search:깊이 우선 탐색)와 BFS(Breadth First Search:너비 우선 탐색)가 있다.
DFS는 stack을 BFS는 queue를 사용하여 각각 구현한다. (stack과 queue에 대해서는 다른 글을 참고)
그래프의 노드를 탐색하기 위해서는 노드간 간선에 의해 연결된 인접한 노드 정보가 필요하며 이 정보들을 행렬(2차원 리스트) 또는 리스트 형태로 저장하여 사용한다. 행렬 형태의 인접 노드 정보를 adjacency matrix라 하고 리스트 형태의 인접 노드 정보를 adjacency list라고 한다. adjacency matrix는 불필요한 정보까지 저장하게 되어 메모리를 낭비하게 되지만 원하는 관계 정보를 빠르게 조회할 수 있다. adjacency list는 matrix와는 반대로 메모리의 낭비는 없지만 원하는 관계 정보를 조회하기 위해 선형으로 조회해야 하기 때문에 속도가 비교적 떨어질 수 있다.
[DFS]
서두에서 DFS는 stack을 사용하여 구현할 수 있다고 언급했다. 프로그래밍 언어의 함수 호출은 stack 구조를 사용하게 되므로 재귀 함수를 사용해서도 DFS를 구현할 수 있다. 여기서는 stack과 재귀 함수 두 가지 방법을 모두 사용하여 구현해보도록 한다. (구현 예제는 유튜버 엔지니어대한민국님의 채널의 내용을 인용했다. - www.youtube.com/user/damazzang 기본 알고리즘의 개념과 구현을 충실하게 다루고 있는 채널이니 학습 시 참고하면 좋을 것으로 생각된다.)
구현에 앞서 DFS의 동작을 이미지로 확인해보자.
1. 시작 노드를 0으로 지정하여 스택에 푸쉬하고 노드 0이 푸쉬되었다는 사실을 해당 노드에 기록한다.
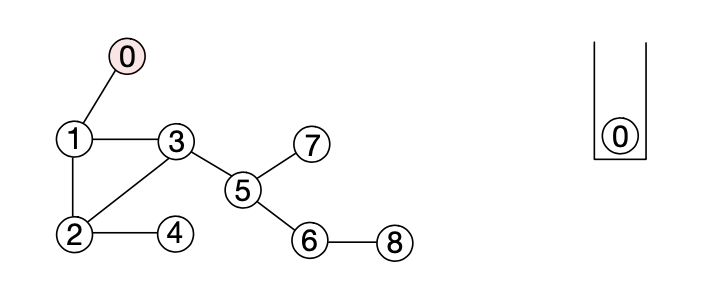
2. 스택에서 노드 0을 팝한 뒤 인접한 노드인 1을 푸쉬하고 노드 1이 스택에 푸쉬되었다는 사실을 해당 노드에 기록한다.
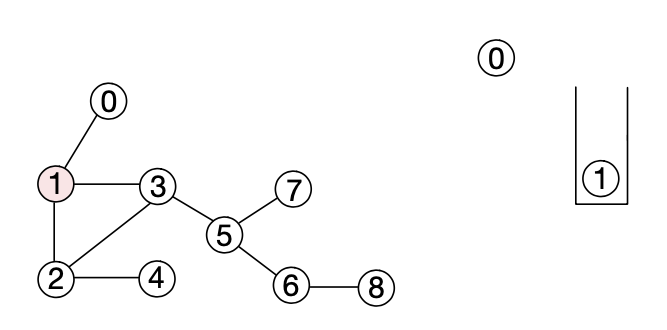
3. 스택에서 노드 1을 팝한 뒤 인접한 노드인 2와 3을 푸쉬하고 노드 2와 3이 푸쉬되었다는 사실을 해당 노드들에 기록한다.

4. 스택에서 노드 3을 팝한 뒤 인접한 노드인 5를 푸쉬하고 노드 5가 스택에 푸쉬되었다는 사실을 해당 노드에 기록한다.

5. 스택에서 노드 5를 팝한 뒤 인접한 노드인 6과 7을 푸쉬하고 노드 6과 7이 푸쉬되었다는 사실을 해당 노드들에 기록한다.
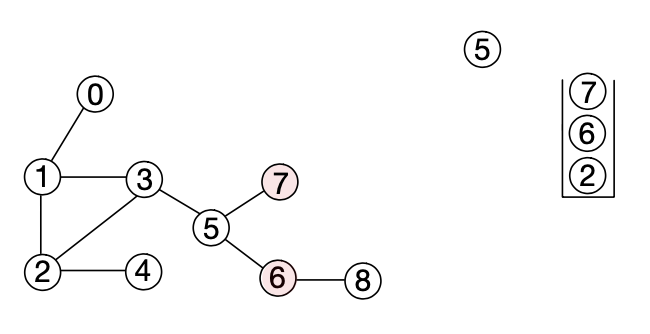
6. 스택에서 노드 7을 팝한다. 인접한 노드 중 스택에 들어간 이력이 없는 노드가 없으므로 푸쉬는 발생하지 않는다.

7. 스택에서 노드 6을 팝한 뒤 인접한 노드인 8을 푸쉬하고 노드 8이 푸쉬되었다는 사실을 해당 노드에 기록한다.

8. 스택에서 노드 8을 팝한다. 인접한 노드 중 스택에 들어간 이력이 없는 노드가 없으므로 푸쉬는 발생하지 않는다.
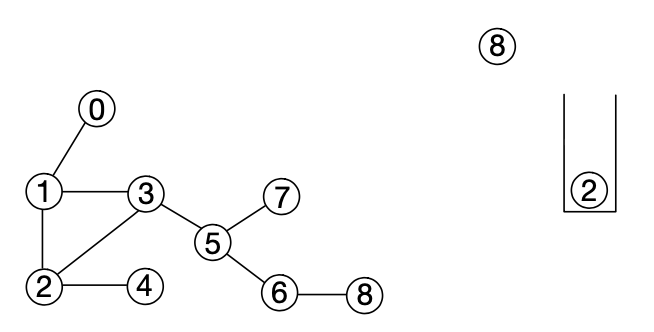
9. 스택에서 노드 2를 팝한 뒤 인접한 노드인 4를 푸쉬하고 노드 4가 푸쉬되었다는 사실을 해당 노드에 기록한다.
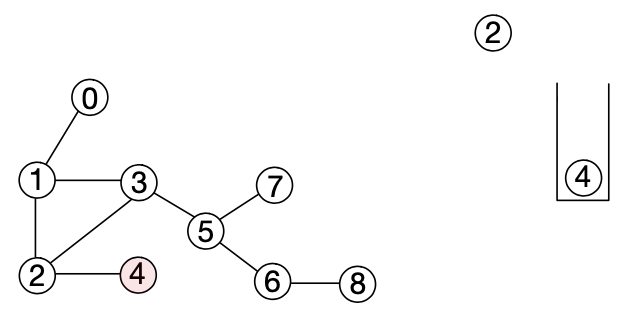
10. 스택에서 노드 4를 팝하면 스택이 비어있게 되며 이는 더이상 탐색할 노드가 없다는 것을 의미하므로 탐색을 종료한다.
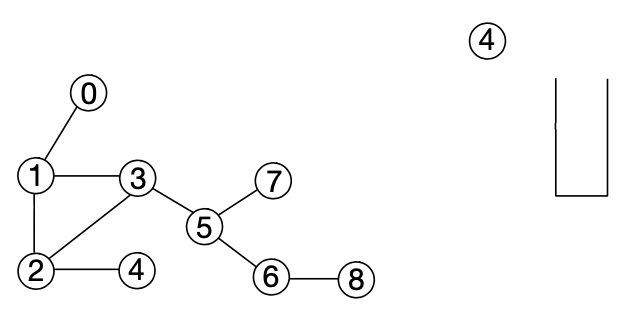
[BFS]
BFS는 일반적으로 DFS에 비해 속도면에서 유리하다 알려져있다. BFS의 구현에는 queue를 사용한다.
구현에 앞서 BFS의 동작을 이미지로 확인해보자.
1. 시작 노드를 0으로 지정하여 큐에 애드한다.
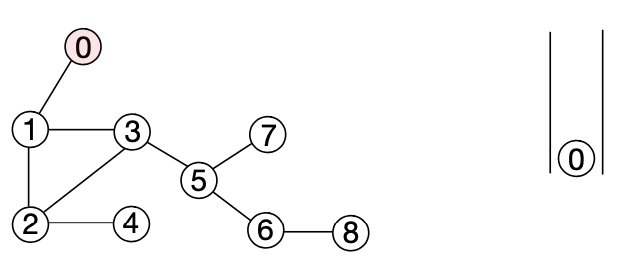
2. 큐에서 노드 0을 리무브한 뒤 인접한 노드인 1을 애드하고 노드 1이 애드되었음을 해당 노드에 기록한다.
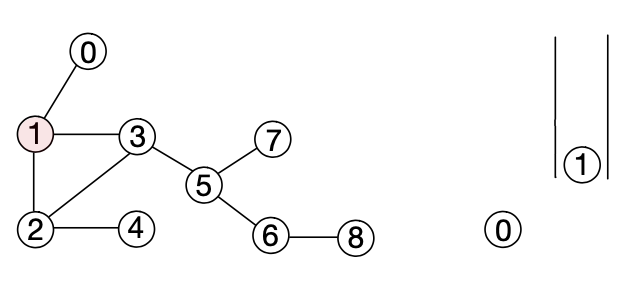
3. 큐에서 노드 1을 리무브한 뒤 인접한 노드인 2와 3을 애드하고 노드 2와 3이 애드되었음을 해당 노드들에 기록한다.
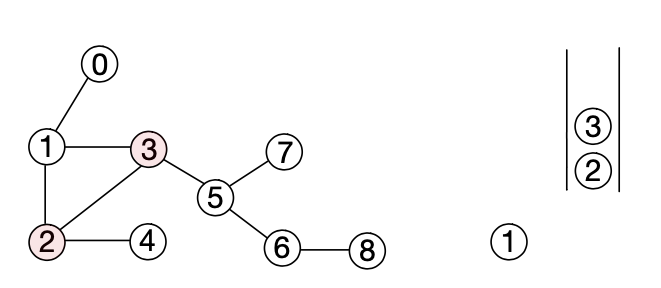
4. 큐에서 노드 2를 리무브한 뒤 인접한 노드인 4를 애드하고 노드 4가 애드되었음을 해당 노드에 기록한다.

5. 큐에서 노드 3를 리무브한 뒤 인접한 노드인 5를 애드하고 노드 5가 애드되었음을 해당 노드에 기록한다.
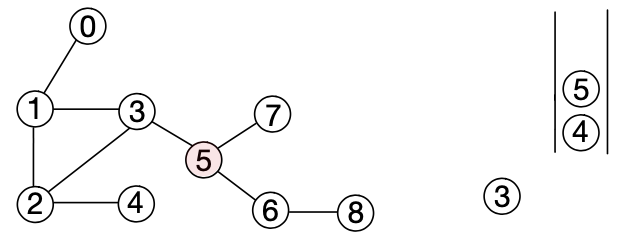
6. 큐에서 노드 4를 리무브한다. 인접한 노드 중 큐에 들어간 이력이 없는 노드가 없으므로 애드는 발생하지 않는다.

7. 큐에서 노드 5를 리무브한 뒤 인접한 노드인 6과 7을 애드하고 노드 6과 7이 애드되었음을 해당 노드들에 기록한다.

8. 큐에서 노드 6를 리무브한 뒤 인접한 노드인 8를 애드하고 노드 8가 애드되었음을 해당 노드에 기록한다.

9. 큐에서 노드 7을 리무브한다. 인접한 노드 중 큐에 들어간 이력이 없는 노드가 없으므로 애드는 발생하지 않는다.

10. 큐에서 노드 8을 리무브하면 큐가 비어있게 되며 이는 더이상 탐색할 노드가 없음을 의미하므로 탐색을 종료한다.

[DFS와 BFS의 구현]
전체코드는 다음 링크에서 확인할 수 있다.
JAVA: github.com/camel-master/GraphSearchWithJAVA.git
Python: github.com/camel-master/GraphSearchWithPython.git
1. JAVA로 구현
import java.util.ArrayList; import java.util.LinkedList; public class Graph<T> { public static class Node<T> { private final T data; private boolean marked; private final LinkedList<Node<T>> adjacent; public Node(T data) { this.data = data; this.marked = false; adjacent = new LinkedList<>(); } } private final ArrayList<Node<T>> nodes = new ArrayList<>(); public Graph(T[] arr) { for(T data : arr) { Node<T> newNode = new Node<>(data); nodes.add(newNode); } } public void addEdge(int i1, int i2) { Node<T> n1 = nodes.get(i1); Node<T> n2 = nodes.get(i2); if(!n1.adjacent.contains(n2)) { n1.adjacent.add(n2); } if(!n2.adjacent.contains(n1)) { n2.adjacent.add(n1); } } public void dfs(int index) { Node<T> root = nodes.get(index); Stack<Node<T>> stack = new Stack<>(); stack.push(root); root.marked = true; while(!stack.isEmpty()) { Node<T> popNode = stack.pop(); for(Node<T> n : popNode.adjacent) { if(!n.marked) { n.marked = true; stack.push(n); } } visit(popNode); } System.out.println(); } public void dfsR(int index) { dfsR(nodes.get(index)); System.out.println(); } public void dfsR(Node<T> node) { if(node == null) return; node.marked = true; visit(node); for(Node<T> n : node.adjacent) { if(!n.marked) { dfsR(n); } } } public void bfs(int index) { Node<T> root = nodes.get(index); Queue<Node<T>> queue = new Queue<>(); queue.add(root); root.marked = true; while(!queue.isEmpty()) { Node<T> removedNode = queue.remove(); for(Node<T> n : removedNode.adjacent) { if(!n.marked) { n.marked = true; queue.add(n); } } visit(removedNode); } System.out.println(); } public void visit(Node<T> n) { System.out.print(n.data + " "); } }2. Python으로 구현
from Stack import Stack from Queue import Queue def visit(n): print(n.data, end=' ') def dfs_recursive(node): if not node: pass node.marked = True visit(node) for n in node.adjacent: if not n.marked: dfs_recursive(n) class Graph: class Node: def __init__(self, data): self.data = data self.marked = False self.adjacent = [] def __init__(self, arr): self.__nodes = [] for data in arr: self.newNode = self.Node(data) self.__nodes.append(self.newNode) def add_edge(self, i1, i2): n1 = self.__nodes[i1] n2 = self.__nodes[i2] if not (n2 in n1.adjacent): n1.adjacent.append(n2) if not (n1 in n2.adjacent): n2.adjacent.append(n1) """ #Implement stack by python list type def dfs(self, index): root = self.__nodes[index] stack = [root] root.marked = True while len(stack) > 0: pop_node = stack.pop() for n in pop_node.adjacent: if not n.marked: n.marked = True stack.append(n) visit(pop_node) print() """ def dfs(self, index): root = self.__nodes[index] stack = Stack() stack.push(root) root.marked = True while not stack.is_empty(): pop_node = stack.pop() for n in pop_node.adjacent: if not n.marked: n.marked = True stack.push(n) visit(pop_node) print() def dfs_recursive_first(self, index): dfs_recursive(self.__nodes[index]) print() def bfs(self, index): root = self.__nodes[index] queue = Queue() queue.add(root) root.marked = True while not queue.is_empty(): remove_node = queue.remove() for n in remove_node.adjacent: if not n.marked: n.marked = True queue.add(n) visit(remove_node) print()'Data Structure & Algorithm' 카테고리의 다른 글
퀵정렬(Quick Sort) (0) 2021.01.28 삽입정렬(Insertion Sort) (0) 2021.01.24 선택정렬(Selection Sort) (0) 2021.01.22 DFS, BFS with python (0) 2021.01.11 Stack과 Queue (0) 2020.09.28